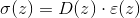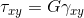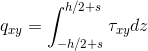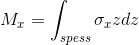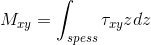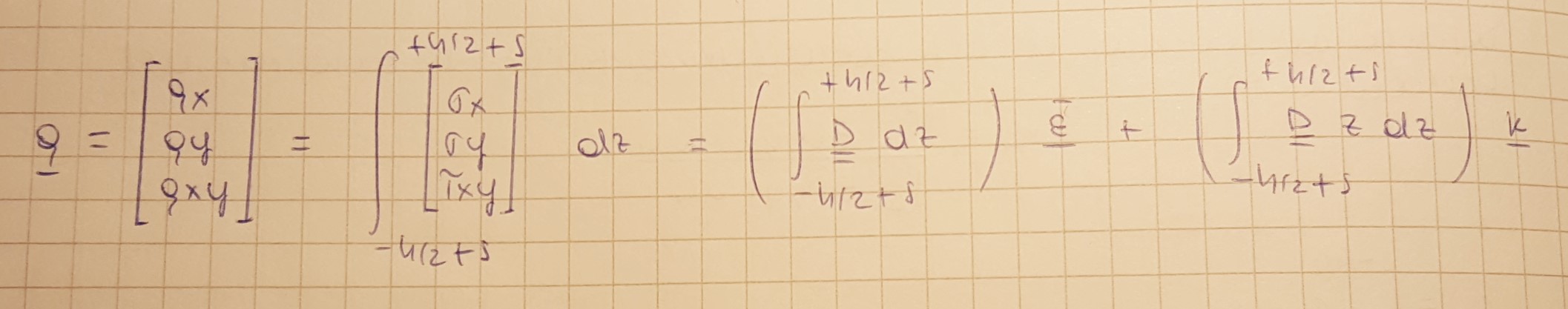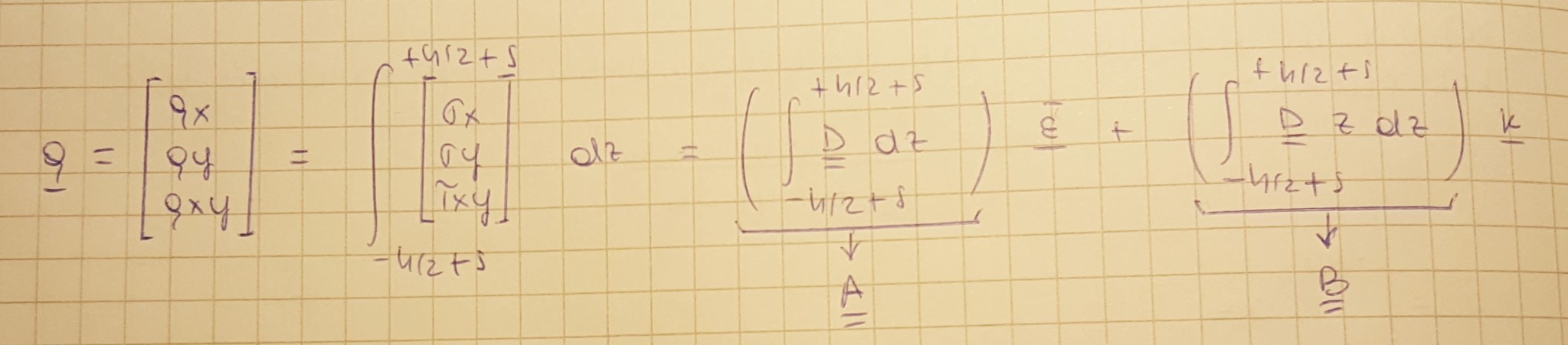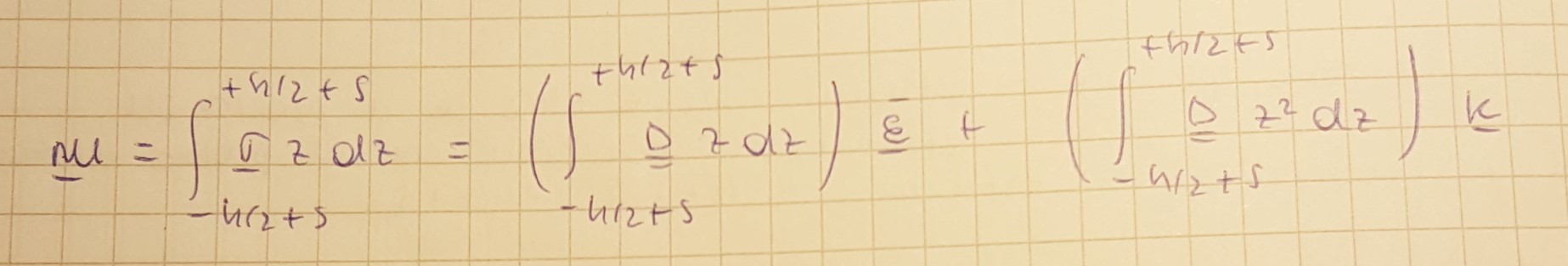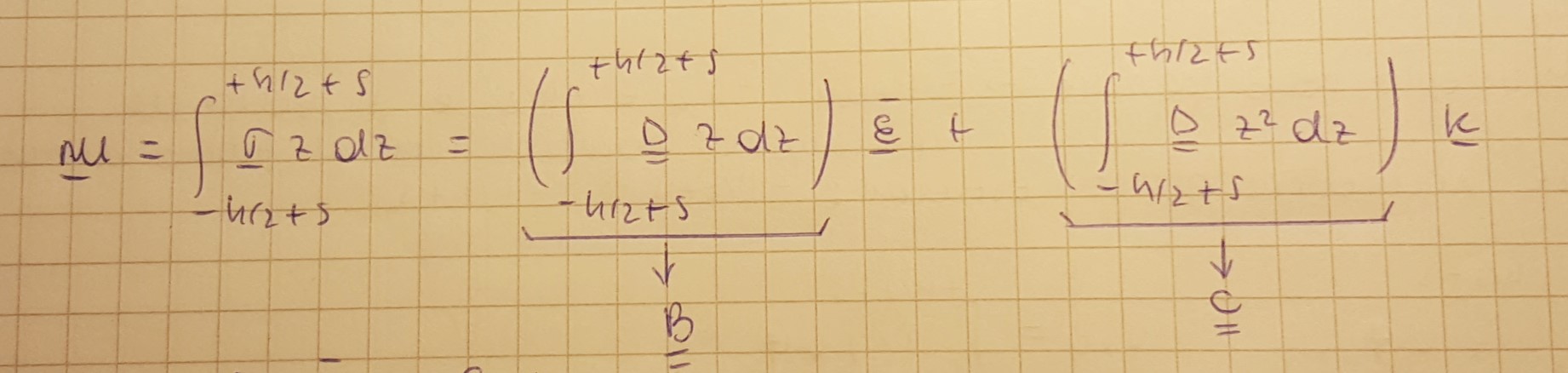Nella scorsa lezione è stata trattata l'ipotesi cinematica applicata al problema delle piastre alla Kirchhoff. Essa prevede che i segmenti sul piano medio di un corpo in parete sottile rimangano rigidi, in particolare rimangano perpendicolari alla superficie media anche nella configurazione deformata. Tenendo conto di questa ipotesi abbiamo ridotto gli spostamenti di un punto generico del materiale elastico come funzione degli spostamenti e delle rotazioni di un punto preso sulla superficie media o di riferimento. Abbiamo quindi spostamenti di ogni punto del corpo risolti in funzione di u̅,v̅,w̅,Θx,Θy (tali quantità sono state prese sul piano di riferimento, che di solito coincide con il piano medio). Derivando abbiamo ottenuto le deformazioni (funzioni di z):

(E' importante tenere a mente che x,y,z sono assi locali e z è localmente perpendicolare alla superficie di riferimento)

Dalla formula si vede che la deformazione lungo lo spessore di piastra è uguale alla deformazione sul piano di riferimento, ε̅ (nel vettore ε̅ mancano la epsilon z che è definita per effetto Poisson e gammayz e gamma zx che sono per ipotesi nulle),più una quota parte lineare, proporzionale a z stesso, moltiplicata per un vettore di curvature.

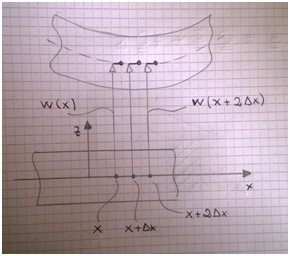
Le curvature sono omogenee lungo lo spessore (uguali su tutti i punti dello spessore) per cui non è importante distinguere se le si prende sul piano di riferimento o fuori da esso. Per quanto riguarda epsilon, invece, è importante distinguere se viene campionato all'interno o al di fuori del piano di riferimento. Tornando a parlare del vettore delle curvature, esso contiene la curvatura attorno a x , la curvatura attorno a y e una mista. Quest'ultima è maggiore di zero quando ho una curvatura visibile se seziono la lastra sul piano xz. Per chiarire questo concetto vediamo la fig.1.

Le frecce in figura indicano gli spostamenti a deformazione avvenuta, ossia w(x) e w(x+Δx).

Fig.1

Presi gli spostamenti w per due punti consecutivi riesco a definire un'inclinazione del piano di riferimento della superficie; presi altri due punti riesco a definire una seconda inclinazione e così ho due derivate prime. Nel caso in figura, avendo a disposizione quei tre punti, per delta x che tende a zero, tramite il rapporto incrementale trovo la derivata seconda, ossia la curvatura:

$$ - k_x = +\frac{\partial}{\partial x} \left( \frac{\partial w}{\partial x} \right) = \frac{\partial^2 w}{\partial x^2} $$

$k_x$ è la variazione di inclinazione del piano tangente alla superficie di riferimento nella configurazione deformata se ci si muove in direzione x, cambiata di segno. La figura infatti rappresenta una curvatura negativa se si utilizza la convenzione “curvatura positiva se fibre a $z>0$ (es. superficie superiore) tese”.(NdEB)

Il legame tra inclinazione della superficie di riferimento sulla deformata e la curvatura è diretto poiché si assume che le due deformazioni taglianti, nel caso specifico ɣxz, siano uguali a zero. Per semplicità si assume che la superficie di partenza sia piana anche se tale teoria può essere applicata nel caso di superficie non piana. Grazie all'ipotesi cinematica fatta in precedenza, possiamo essere certi che l'andamento della deformazione è sempre lineare, anche nel caso di materiale anisotropo.

Una volta note le deformazioni, possiamo trovare le tensioni, anch'esse funzioni di z ma non più lineari lungo spessore a meno che il materiale non sia omogeneo lungo lo spessore.

D è la matrice del legame costitutivo, in uno stato di tensione piana e per un materiale omogeneo isotropo, mentre ε è il vettore delle deformazioni.

Da questa possiamo risalire alla solita relazione :

Naturalmente se il materiale non è omogeneo, il modulo di Young, E, ed il coefficiente di Poisson sono funzione di z. A questo punto possiamo scrivere le tensioni lungo lo spessore, in questo modo:

Il secondo termine corrisponde allo stato tensionale dovuto alle curvature (che varia lungo lo spessore in virtù della posizione del punto e della variazione della matrice D); il primo corrisponde allo stato tensionale dovuto alla deformazione del piano di riferimento, definita DEFORMAZIONE MEMBRANALE (che varia lungo lo spessore solo in virtù della variazione della matrice D). Il concetto di deformazione membranale può essere utilizzato solo se il piano di riferimento coincide con il piano medio ed/o il materiale è simmetrico rispetto a questo piano di riferimento. (*Per chiarimenti sulla deformazione membranale vedi fine pagina)

Torniamo ora alle tensioni. Grazie all'ipotesi cinematica non è necessario calcolare il valore degli spostamenti punto per punto sullo spessore. Tale ipotesi può valere anche per le tensioni, che possiamo considerare come quantità integrate:

L'integrazione avviene lungo lo spessore solo se il piano di riferimento coincide con il piano medio. Se così non fosse e i due piani rimanessero distanti di una certa quantità, s, allora dovremmo aggiungere questa quantità agli estremi di integrazione.

È possibile trovare un piano medio migliore di altri?

Presa una sezione di trave si definiscono due assi di appoggio ξ ed ζ e cerco un punto in cui, applicando uno sforzo normale, non si abbiano curvature. La posizione di tale punto è la media pesata delle coordinate ξ lungo la sezione ed è funzione dell'unico modulo di Young di interesse per la sezione, ossia quello in direzione assiale.

Nel caso della piastra potrei trovare un piano di riferimento tale per cui le sollecitazioni che vengono applicate su questo piano non inducono curvatura. Cerco il punto tale per cui:

la coordinata ζ è uguale all'integrale lungo lo spessore del modulo di Young per ζ in dζ fratto il modulo di Young medio.

Se il materiale fosse isotropo e caratterizzato da un solo modulo di Young, tale ragionamento potrebbe andare bene poiché in questo modo potremmo definire univocamente la quota ζ del piano medio. In realtà potrebbe capitare che i moduli di Young siano diversi in direzione entro piano e fuori piano (ad es. in un materiale composito). Inserendoli negli integrali troverei un piano di riferimento corretto per le sollecitazioni che agiscono lungo x ed un piano di riferimento adatto per le sollecitazioni che agiscono lungo y. Non posso trovare quindi un piano di riferimento migliore degli altri perché questo non sarebbe comunque univoco rispetto alla direzione della sollecitazione: qualsiasi piano ha lo stesso “valore” rispetto agli altri. Nel caso della trave, qualunque sia lo stato di anisotropia, l'unico modulo di Young di interesse è quello assiale ed è più facile trovare un punto in cui far passare uno sforzo normale senza l'insorgenza di curvature, nonostante ad es. le possibili deformazioni a taglio. Se il materiale non è omogeneo troviamo maggiore difficoltà a scegliere un piano medio migliore degli altri per cui va bene sceglierne uno arbitrariamente.

Comunque, svolgendo gli integrali si ottengono le CARATTERISTICHE di SOLLECITAZIONE.

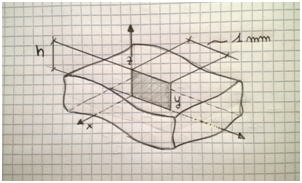
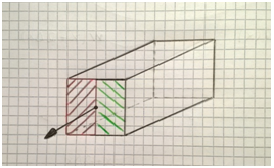
Prendiamo una piastra (fig.2) e facciamo un taglio perpendicolare all'asse x. Prendiamo una superficie all'interno della piastra, di altezza h (pari allo spessore della piastra) e lunghezza unitaria.

fig.2

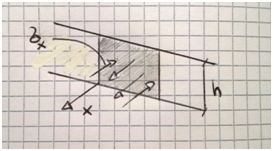
Ingrandendo si possono vedere le σx entranti e uscenti, perpendicolari alla superficie (fig.3):

fig.3

qx è la risultante delle azioni in direzione x che vengono scambiate dal materiale su quella superficie. Essa è una forza su mm poiché è la forza sullo spessore. Ragionamenti analoghi possono essere fatti con qy e qz. Se svolgo gli stessi integrali considerando anche il braccio della forza ottengo i momenti:

questi sono i momenti risultanti dalle tensioni applicate sulle facce ottenute da specifici tagli effettuati sulla piastra. Mx è il momento risultante delle σx che agiscono sulla faccia di fig.3

Abbiamo a questo punto ricavato delle relazioni tra le quantità di tipo deformativo ε e k, con il vettore delle tensioni q, ed il vettore dei momenti M. La relazione relativa al vettore q si ottiene abbastanza semplicemente sostituendo sigma nell’ integrale che definisce le tensioni.

ε e k sono fuori dal segno dell’ integrale perché oggetti costanti lungo lo spessore. Questo è un integrale di matrici, definito come una matrice i cui termini sono gli integrali dei termini della matrice integranda. Se D varia senza nessuna legge nello spessore, data l’assenza di una qualsiasi legge di tipo polinomiale, è necessario effettuare un’ integrazione che non sarà mai precisa, qualunque sia il numero di campionamenti o la tecnica utilizzata; se la variazione di D lungo lo spessore è meno arbitraria, ad esempio il materiale è stratificato o quantomeno omogeneo a tratti, per svolgere in maniera esatta l’integrale si prendono su ogni tratto due punti di Gauss. È possibile procedere all’ integrazione esatta di questo oggetto in alcuni casi ristretti: sezione omogenea o omogenea a tratti. Questa matrice si riduce ad una forma molto più semplice se il materiale è omogeneo e isotropo.

Considerando il materiale omogeneo in z, il primo integrale è la matrice A=D*h e il secondo integrale è denominato in generale matrice B; se il materiale è omogeneo e se non c’è scostamento (s=0), allora B=0 perché integro una quantità costante: i contributi per z positivo sono uguali e contrari a quelli per z negativo. Posso quindi dire semplicemente che q è uguale a

Nel caso specifico (materiale omogeneo in z e piano di riferimento coincidente con il piano medio) A e B hanno andamenti abbastanza semplici.

È possibile scrivere una relazione che leghi le quantità di tipo deformativo ed i momenti:

Volendo ottenere una forma del tipo

procedo nella stessa maniera precedente. Il primo integrale coincide con la matrice B già trovata nella relazione delle tensioni, il secondo integrale è la matrice C; se il materiale è omogeneo e D è costante in z, risulta che 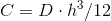, e questo vale sia per s = 0 che per s ≠ 0.

Completato il legame lineare tra caratteristiche di sollecitazione e caratteristiche di deformazione specifiche per la piastra, è possibile ottenere quindi un’ unica relazione data da

Nel caso di materiale omogeneo lineare elastico, se s=0 (piano medio e piano di riferimento coincidono), la relazione sarà data da

Come evidenziato in figura, possiamo notare che è presente una matrice di tipo rigidezza (lega delle sollecitazioni a delle deformazioni) che definisce quali sono le sollecitazioni da applicare alla piastra per ottenere una data deformazione. Analizziamo questa matrice rigidezza per materiali omogenei lungo lo spessore (non è necessario che siano anche isotropi, il materiale può essere generico) . Nel caso di materiale omogeneo quindi, per ottenere ad esempio una curvatura è necessario applicare solo momenti e non azioni membranali perché essendo B=0(matrice B: termini di accoppiamento tra deformazioni al piano di riferimento con i momenti e curvature al piano di riferimento con le sollecitazioni membranali), si ha che 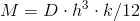. Fatte queste considerazioni, si ottiene quindi che i due problemi, membranale e flessionale, sono distinti: se applico dei momenti ho solo curvature e se ho azioni membranali ottengo solo allungamenti del piano di riferimento. Abbiamo inoltre definito altri due termini: la matrice D*h che si presta ad essere chiamata termine di rigidezza membranale della piastra, in quanto lega le deformazioni al piano di riferimento (che in questo caso coincide con il piano medio, s=0) alle azioni di tipo membranale. Il termine 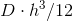si presta ad essere chiamato, invece, rigidezza flessionale e lega le curvature ai momenti applicati. È importante notare che lo spessore della piastra entra in questi due termini in potenze diverse, in particolare entra linearmente nella definizione di rigidezza membranale della piastra, ma entra con potenza terza nella definizione di rigidezza flessionale. Ciò vuol dire che se raddoppio lo spessore, a parità di sollecitazioni membranali q, ho deformazioni membranali dimezzate e quindi la piastra ha rigidezza doppia dal punto di vista membranale; a parità di momenti M ho curvature pari ad 1/8 delle precedenti. Questo vale per tutte le piastre omogenee, in particolare anche per quelle omogenee isotrope.

Vediamo un esempio su una struttura elementare per confrontare le due teorie e vedere le differenze di implementazione dei codici. Utilizzando il modello di Kirchhoff:

Fig.6

Come si vede dall'immagine (fig.6)(in corrispondenza degli elementi i,l,j,k) prendiamo gli elementi quadrilateri 4 nodi che sono i più usati in quest'ambiato e quelli che si prestano meglio. Imponiamo una deformazione come quella in figura, la teoria di Kirchhoff tiene conto delle rotazioni quindi possiamo imporre quattro condizioni al contorno (quelle tra parentesi graffe in figura). L'equazione che descrive la configurazione deformata è del tipo:

se invece utilizziamo il modello di Mindlin:

Fig.7

Con il modello di Mindlin le rotazioni non possono essere utilizzate per arricchire gli spostamenti, per cui si ottiene una pura deformata a taglio (fig.7) e l'equazione che la descrive è lineare del tipo:

Vediamo un esempio esplicativo

fig.8

Supponiamo di prendere un concio di trave molto lungo (fig.8), fatto di un materiale non omogeneo: acciaio da un lato (parte rossa) e alluminio dall'altro (parte verde). In questo caso il baricentro sarà spostato dalla parte dell'acciaio. Consideriamo ora che la trave sia fatta di acciaio e di un mix di alluminio e piombo tale per cui la densità del mix è uguale a quella dell'acciaio. In queste condizioni, il baricentro inteso come centro di massa può essere spostato nel centro (come dovrebbe essere se il materiale fosse omogeneo). Supponiamo di applicare un carico di puro sforzo normale nel baricentro. Tale carico incurverà la trave poiché il modulo di Young del mix è minore di quello dell'acciaio. In questo caso non possiamo parlare di deformazione membranale.

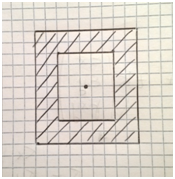
Se invece prendiamo in considerazione una sezione di acciaio cava (fig.9) al cui interno è presente aria e applichiamo uno sforzo normale nel baricentro, esso non determinerà curvatura poiché, anche se non è c'è omogeneità di materiali, la sezione presenta proprietà di simmetria.

fig.9

{ :wikipaom2017:img_18.png?400|}}