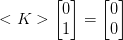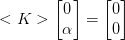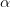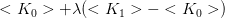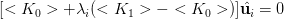Ai fini della trattazione le matrici sono identificate con il simbolo <>.

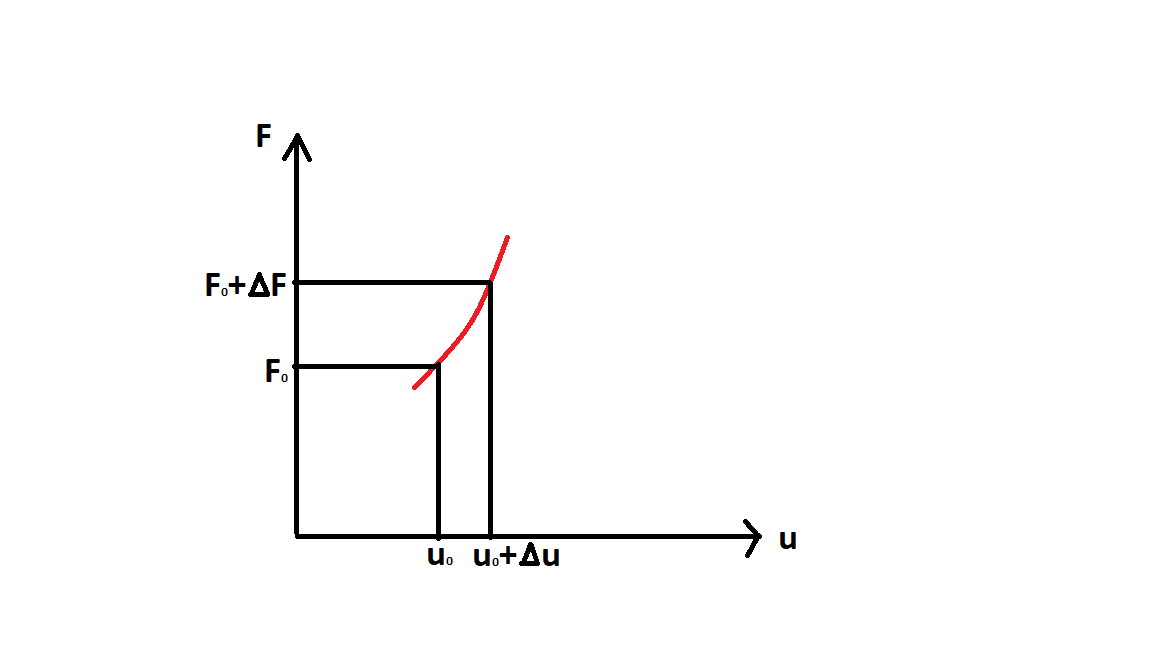
L'instabilità è un fenomeno che si manifesta in situazioni di non linearità geometrica. Per lo studio di questo fenomeno, si considera un sistema a comportamento non lineare, ad un grado di libertà (lo spostamento u); su questo sistema è applicata una forza F; l'andamento è ipotizzato non elastico.

Non è detto che ci sia un unico punto di massimo carico sostenibile dalla struttura, come mostrato in figura. I fenomeni non lineari si hanno nel caso in cui la struttura è soggetta a grandi rotazioni, quindi non valgono più le approssimazioni per cui sen(θ)~θ e cos(θ)~1. Sviluppando in serie di Taylor i termini seno e coseno si ha che la relazione sen(θ)~θ è ancora valida, se si trascurano i termini di ordine superiore al secondo, mentre . Se non si inseriscono i termini superiori al primo ordine, non si osservano fenomeni di instabilità. Si considera un primo livello di carico 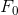, da cui si prende un livello di spostamento 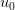e una matrice di rigidezza tangente 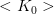che in caso unidimensionale è uno scalare 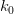(già incontrata come matrice jacobiana della funzione residuo). La matrice di rigidezza tangente indica in che modo il sistema reagisce a variazioni di carico rispetto alla condizione 0. Si suppone di applicare un carico leggermente incrementato; la matrice di rigidezza lega l'incrememto di carico alla variazione di configurazione della struttura.

Si dimostra che , con 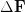che può essere una variazione di carico ma anche, ad esempio, una variazione dello spostamento imposto. Si considera un secondo livello di carico; si ha una seconda matrice di rigidezza tangente. Per un certo livello di carico, si ha la singolarità della matrice di rigidezza tangente: si ha un punto critico (in caso unidimensionale si ha che 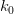=0 ma in caso multidimensionale si può avere singolarità della matrice senza che essa abbia ogni termine nullo). Nell'intorno della condizione critica, si ha la caratterizzazione dello stato C, avente 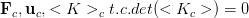. Nello stato C si ha che a fronte di piccole perturbazioni di carico si hanno piccole deformazioni. Il sistema risulta 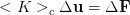e si nota che è in forma non omogenea. Con ipotesi di <K> non singolare, se scrivessi che 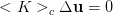, risulta che se non varia il carico non può variare lo spostamento. Tenendo il carico costante e pari al carico critico, esistono invece soluzioni non banali dell'equazione omogenea, essendo la matrice di rigidezza nulla: può esistere almeno uno spostamento non nullo a fronte di variazione di carico nulla. Questo si verifica con molta più frequenza nei casi multidimensionali rispetto al caso monodimensionale. Ad esempio, si può avere la possibilità di un moto di entità arbitraria in 2D,

ma anche

, con quantità arbitraria.

A fronte di un certo carico, si ha una determinata matrice di rigidezza tangente. Arrivati al carico , si suppone di caricare ulteriormente la struttura. Si suppone di avere un carico pari a 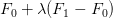. Quale matrice di rigidezza tangente è associabile a questo carico? Si procede ad un'estrapolazione lineare del carico 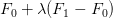e della corrispettiva matrice di rigidezza tangente, trovando che è pari a

Se il salto tra i due carichi non è alto, la relazione di cui sopra è quasi corretta.

Quando ?

Si trovano degli autovalori e autovettori tali che

è soluzione del problema senza incremento di carico. Considerando valida questa estrapolazione lineare del comportamento della matrice di rigidezza tangente, si trovano dei fattori moltiplicativi dell'incremento di carico che danno comportamento critico; si trovano le forme di soluzione che risolvono l'omogenea associata; le soluzioni possono essere sovrapposte in quantità arbitraria alla soluzione base anche senza variare il carico.

Si definisce quindi il carico critico tramite 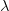; il carico critico può essere combinazione lineare di più carichi incrementati dello stesso fattore .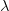