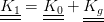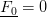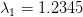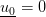Stabilità della trave flessionale a carico assiale
Nei corsi passati abbiamo visto come si comporta un determinato provino, a caratteristica elastica, sotto carichi di trazione. Si distinguono dunque due grafici di risposta elastica, uno dato dalle σ,ε ingegneristiche e l'altro dalle σ,ε vere.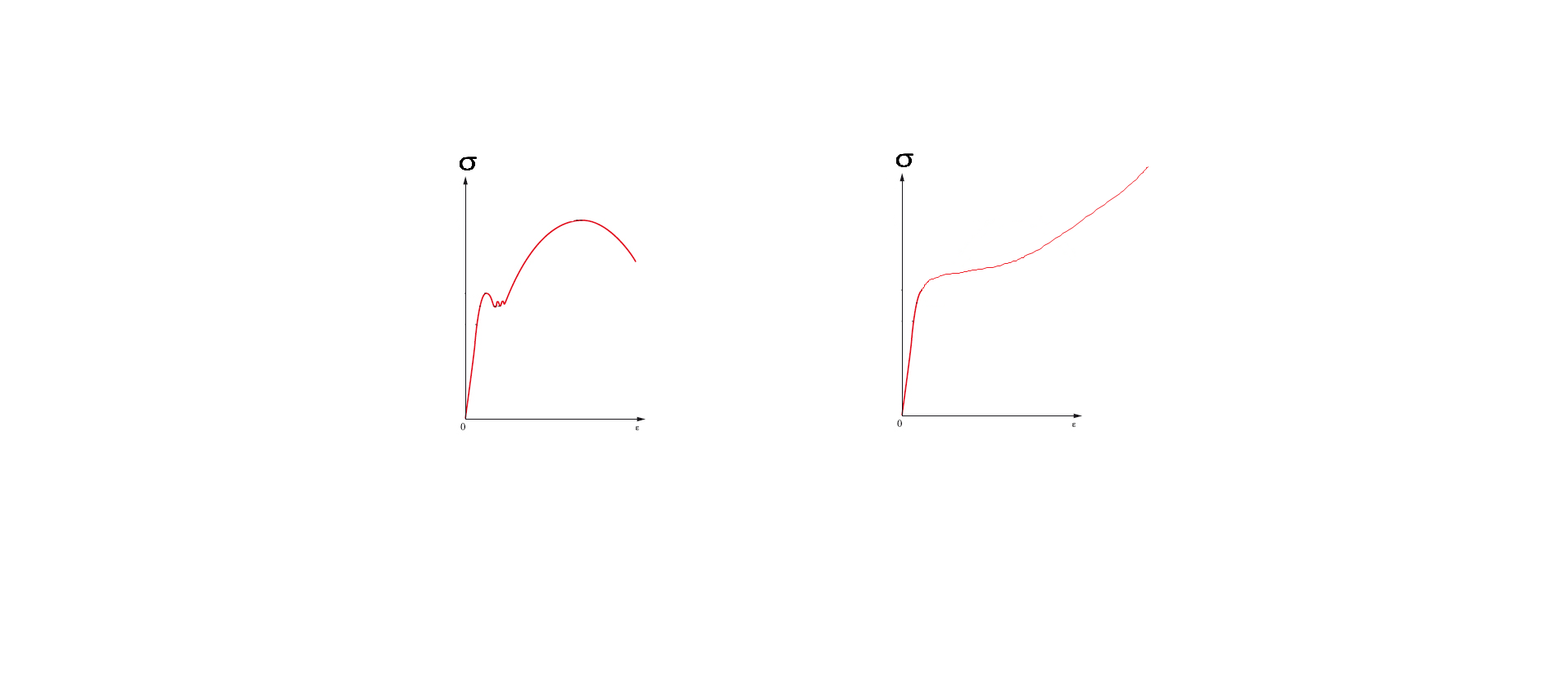
Solitamente, nell'implementazione comune, lo step 0 è quello scarico, quindi ho spostamento nullo e forze applicate nulle, mentre lo step 1 è la struttura caricata da una forza 
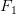che genera uno spostamento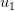 
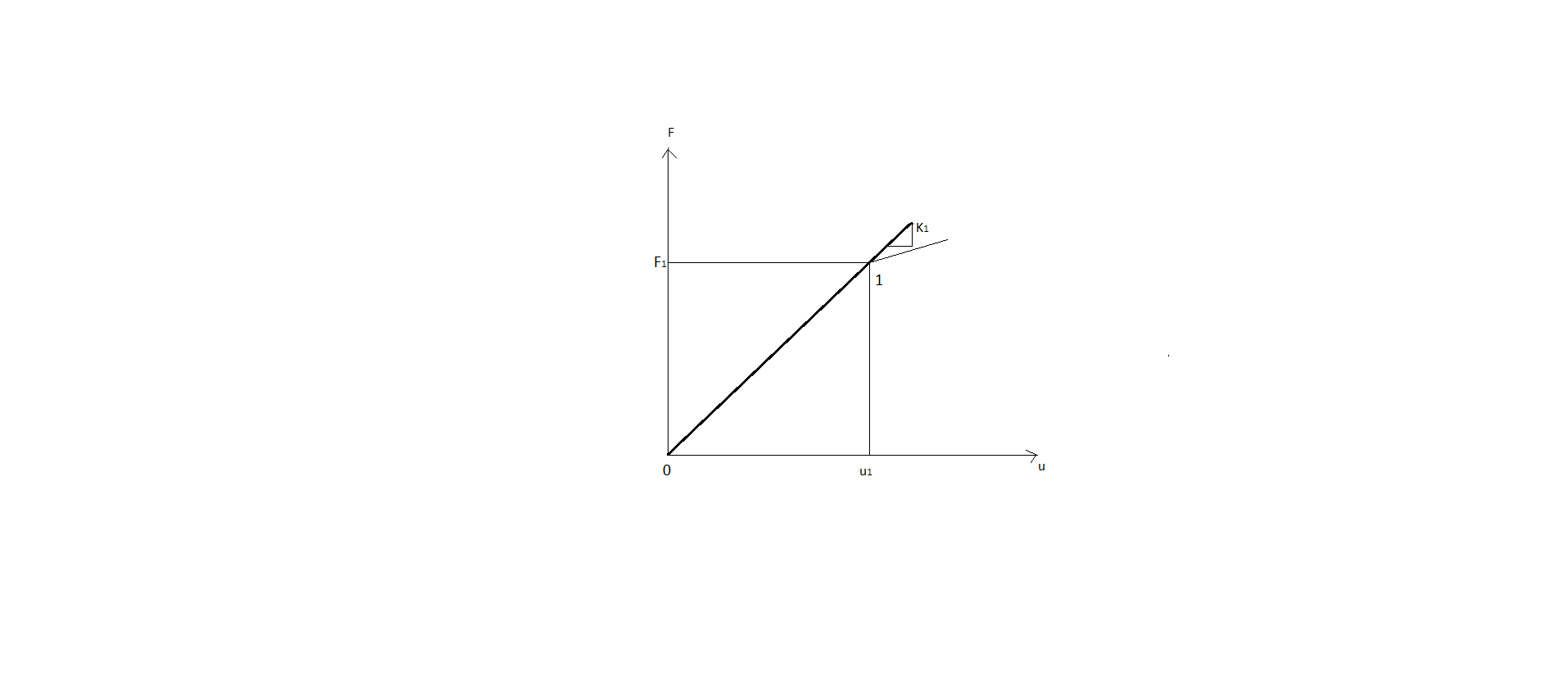L' idea è quella di andare da 1 a 0 con lineare elasticità.
La differenza tra le matrici 
- 
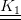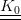è chiamata matrice geometrica 
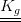, è funzione dei carichi e contiene il contributo dello stato precaricato all' istante 1.
Allora posso dire che:
Instabilità in MARC, modellazione simil NASTRAN
Definiamo un sistema di vincoli e carichi per lo step 0, fase INITIAL LOAD.
Il MARC calcola la struttura sotto i carichi iniziali dati, ci troviamo nello step 1: punto 1 di riferimento della secante → tira fuori .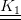
Per 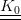: la prende dai vincoli dello step 0 in forma omogenea e senza carichi.
infine accediamo un LOAD CASE “BUCKLING” che fa l'analisi degli autovalori ed autovettori. Questo restituisce come output λ, per ogni grado di libertà disponibile. Tra tutti i λ è importante quello minimo in modulo o il minimo tra i positivi (se il carico è invertibile).
Vediamo un esempio pratico per chiarezza:
si prenda una trave semplicemente incastrata con massa attaccata in estremità
Esiste un carico critico associato a un modo deformativo tale che λ<0.
Se siamo certi che λ non cambia di segno, allora posso scartare i λ<0.
- Esempio numerico 1:
= 1000 [N].
Se escono
ecc..
la stima per il carico critico 
è: = 1234.5 [N].
L' autovalore dunque dà il fattore di amplificazione dell'incremento di carico che porta al carico critico, mentre l'autovettore fa vedere la soluzione che appare per problemi omogenei nell'intorno della criticità.
Il metodo fallisce quando, ad esempio:
da questa configurazione si va a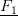 
e 
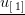
sono gli autovettori usciti dalla matrice rigidezza, nell'intorno di questa condizione.
Questo metodo ha buona predizione del carico critico se ⊥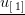 
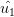, cioè se <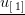, 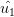> ~ 0 , cioè classici casi di instabilità euleriana.
- Esempio 2:
primo fattore di amplificazione costante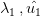 
Considerando F = 1000 [N] e una trave di rigidezza pari a EJ, ottengo un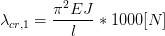 
.
Il caso A presenta una deformata laterale con spostamento 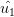; il caso B presenta anch'esso una soluzione elastica (estremo secante) con abbassamenti dei nodi di quantità .
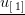Il prodotto scalare tra questi campi di spostamento è esattamente zero, in quanto ortogonali.
- Esempio 3:
nel seguente esempio sono rappresentate due molle unite tra loro da cerniere mobili. Sulla cerniera non vincolata al suolo agisce una forza pari a F. Gli spostamenti concessi avvengono nel piano, quindi in direzione verticale avremo uno spostamento pari a v e in orizzontale u, abbiamo dunque 2 gradi di libertà.
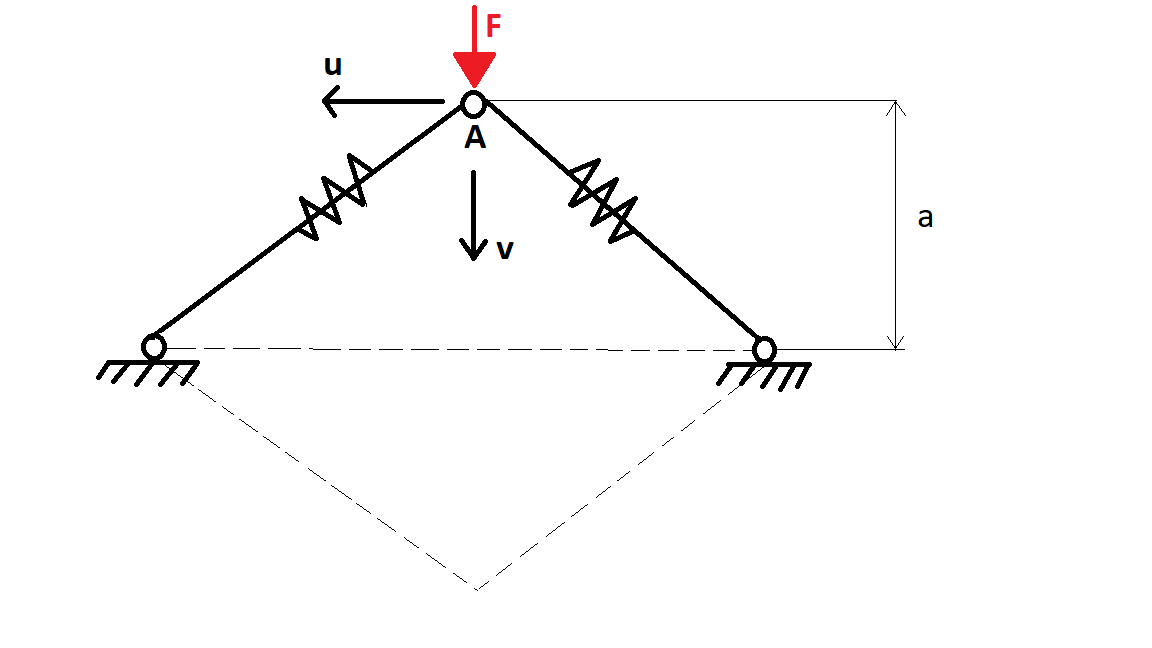Una volta applicata la forza, le due molle inizieranno a comprimersi fino ad arrivare ad un punto in cui la F non serve più perché l'equilibrio (instabile) è garantito dalle reazioni orizzontali delle cerniere.
Possiamo rappresentare graficamente lo spostamento verticale v in funzione della forza F.
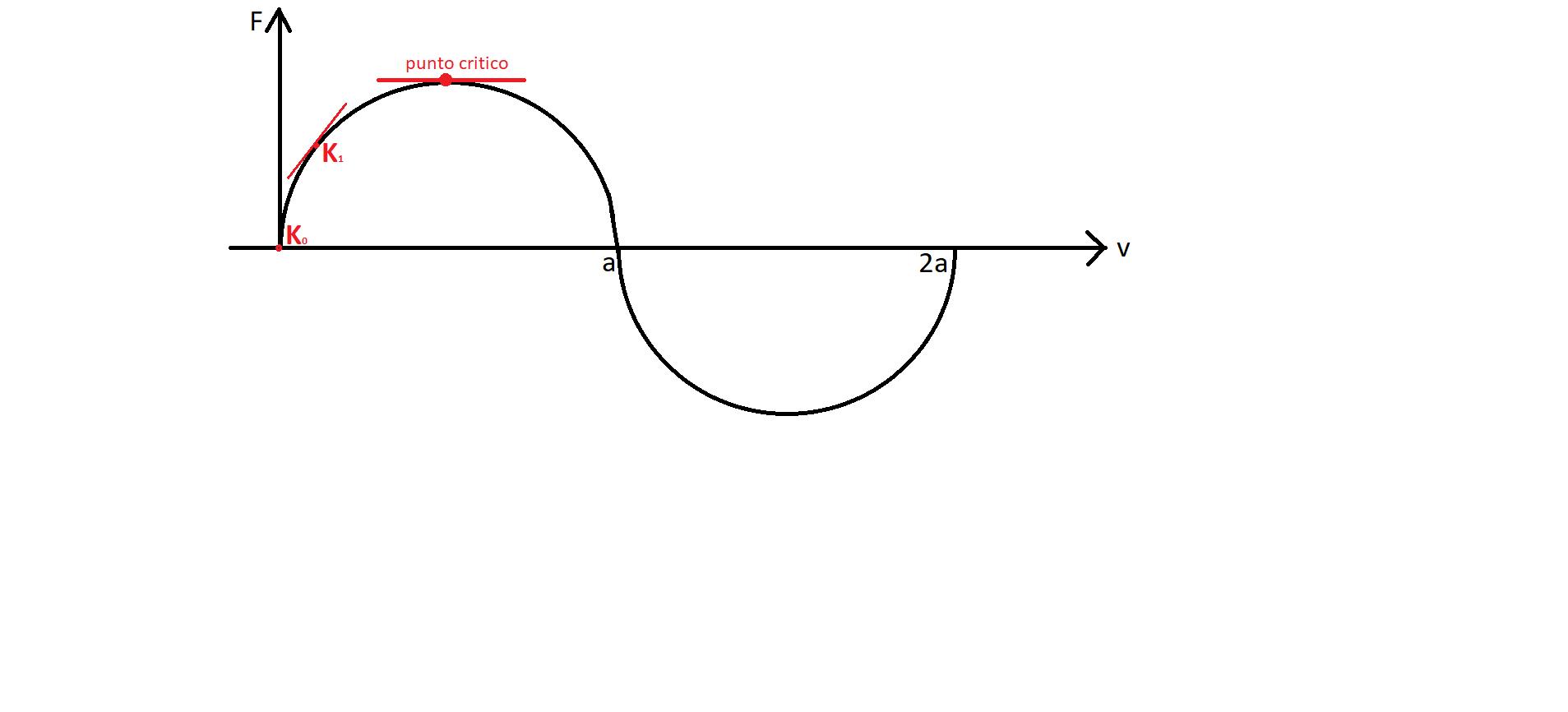La curva nel piano v,F raggiunge il punto “a” quando le due molle entrano in equilibrio instabile. Affinché questo sia mantenuto, quando i due elementi vanno sotto al piano orizzontale la forza deve cambiare di segno. Ecco perché il grafico prosegue nella parte negativa delle ordinate.
Supponiamo ora di voler calcolare 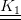tramite 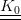: così facendo sovrastimiamo troppo il sistema, cioè 
!
Questo accade perché lo spostamento sotto caso sarà:
= (0,γ) con γ = spostamento verticale generico.
Mentre nel caso di equilibrio orizzontale:
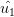= (0,β) questo è dato dal fatto che il moto critico è quello verticale.
I due vettori dunque non sono ortogonali ⇒ l'autovettore che restituisce l'analisi non è affidabile.
Il discorso funziona SOLO se sono in prossimità del punto critico.