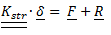Finora si è realizzato l’assemblaggio della matrice di rigidezza della struttura a 5 nodi seguente:

Si procede con l’imposizione di vincoli esterni, condizione necessaria per eliminare la singolarità della matrice di rigidezza per ottenere una soluzione unica; data l’assenza di un vincolamento esterno infatti non risulta univocamente definito il problema degli spostamenti. Consideriamo il seguente sistema:

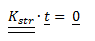
In cui 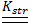rappresenta la matrice di rigidezza della struttura e il vettore degli spostamenti nodali riferito ai tre possibili moti nel piano: traslazione lungo l’asse x, traslazione lungo l’asse y e rotazione intorno all’asse z. Tale sistema descrive un’applicazione lineare che trasforma tre vettori indipendenti a zero. Con struttura non vincolata, se esiste un vettore 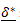soluzione del sistema: 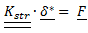risultano essere soluzione anche tutti i vettori nella forma ovvero le combinazioni lineari dei tre moti di corpo rigido; in questo caso esistono $ \infty ^{3} $ soluzioni del problema elastico.

Si sceglie, per esempio, un sistema di vincoli che limiti la traslazione lungo x e y tramite due carrelli posti con assi ortogonali sul nodo 4, ed un ultimo carrello che limiti la rotazione intorno all’asse z posto sul nodo 1. Riferendosi al sistema struttura completo dei carichi agenti $ \underline{F} $ e delle reazioni vincolari $ \underline{R} $ si può scrivere l’equazione:

Si analizza il carrello lungo x: la reazione che questo esercita sarà pari in modulo a qualunque disequilibrio assorbito sul quarto nodo nella medesima direzione; ciò permette di poter togliere direttamente l’equazione di equilibrio ad esso corrispondente nella matrice. Si sostituisce agli ‘slots’ della settima riga di 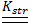tranne per il settimo posto che va a moltiplicare lo spostamento nodale $\underline{u_{4}} $ del vettore $\underline{\delta} $ che si pone unitario. Si ottiene una matrice nella forma:

Così facendo però si perde la simmetria della 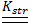per utilizzare solutori e sistemi di stoccaggio più efficienti è opportuno ripristinare la simmetria della matrice. Si pone perciò anche la settima colonna della matrice piena di zeri, tranne per il settimo posto. Perché sia lecito questo passaggio si considerano tutti gli elementi di tale colonna moltiplicati per lo spostamento nodale $\underline{u_{4}} $ del vettore $\underline{\delta}$, il quale risulta determinato una volta imposto il vincolo esterno. Nel vettore dei termini noti infatti è pari ad una generica quantità $\overline{u_{4}}$ , che per la struttura vincolata coincide con zero. Per riportare la simmetria allora sarà sufficiente moltiplicare tutti gli elementi non nulli della settima colonna per $\overline{u_{4}}$, cambiarli di segno e spostarli a destra dell’uguale, aggiornando il vettore dei termini noti. La matrice così ottenuta sarà del tipo:

Allo stesso modo si procede per la traslazione lungo y , azzerando ottava riga e ottava colonna della matrice e per la rotazione intorno a z, azzerando la seconda riga e la seconda colonna della matrice. Si ottiene una nuova forma della matrice di rigidezza $\underline{K_{v}}$ del sistema vincolato. Il sistema totale sarà nella forma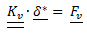

Dove $\underline{\delta}$ è il residuo, cioè il vettore, da determinare, che contiene la soluzione in termini di spostamenti nodali del problema con vincolo e $\underline{F_{v}}$ è il vettore finale dei termini noti comprensivo dei carichi esterni e degli spostamenti imposti, da cui dipende. Per determinare il residuo è sufficiente scomporre la matrice nel prodotto di due matrici triangolari, una la trasposta dell’altra:

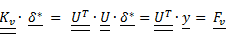
Prima si risolve il sistema $ \underline{\underline{U}}^{T}* \underline{y}= \underline{F_{v}}$ derivandone il vettore soluzione $ \underline{y^{*}}$ in maniera semplice in quanto la matrice $\underline{U}^{T}$ è triangolare inferiore; ora si può risolvere il secondo sistema e determinare il vettore degli spostamenti nodali cercato. Va notato che la matrice di rigidezza del sistema vincolato è solo funzione della mesh e dei gradi di liberta vincolati, quindi una volta scomposta il metodo di soluzione del problema elastico sarà lo stesso, anche variando i carichi esterni o gli spostamenti imposti. Per determinare infine le reazioni vincolari basta risolvere il seguente sistema: 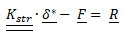Dove $ \underline{K_{str}}$ è la matrice di rigidezza della struttura non vincolata assemblata in partenza, $ \underline{\delta ^{*}}$ il residuo e $ \underline{F}$ il vettore dei carichi esterni iniziale.