Indice
CONSIDERAZIONI SULL'ANALISI DINAMICA DELLA MOLLA CON E SENZA SMORZAMENTO
Le seguenti considerazioni saranno riferite ad una molla a filo cavo sottoposta ad un'analisi dinamica e aventi le caratteristiche decritte in tabella:
| raggio medio | 20 mm |
| passo | 15 mm |
| diametro esterno filo | 12 mm |
| diametro interno filo | 6 mm |
| numero spire | 4.5 |
| materiale | Titanio |
| spostamento armonico imposto all'estremo | ampiezza 1 mm |
La molla è vincolata all'estremo superiore da un incastro e all'inferiore da una coppia prismatica, come rappresentato in figura.


Valutazione del carico a bassa frequenza
Come si può osservare dal seguente grafico, la risposta dinamica del sistema eccitato a basse frequenze è molto simile alla risposta statica.
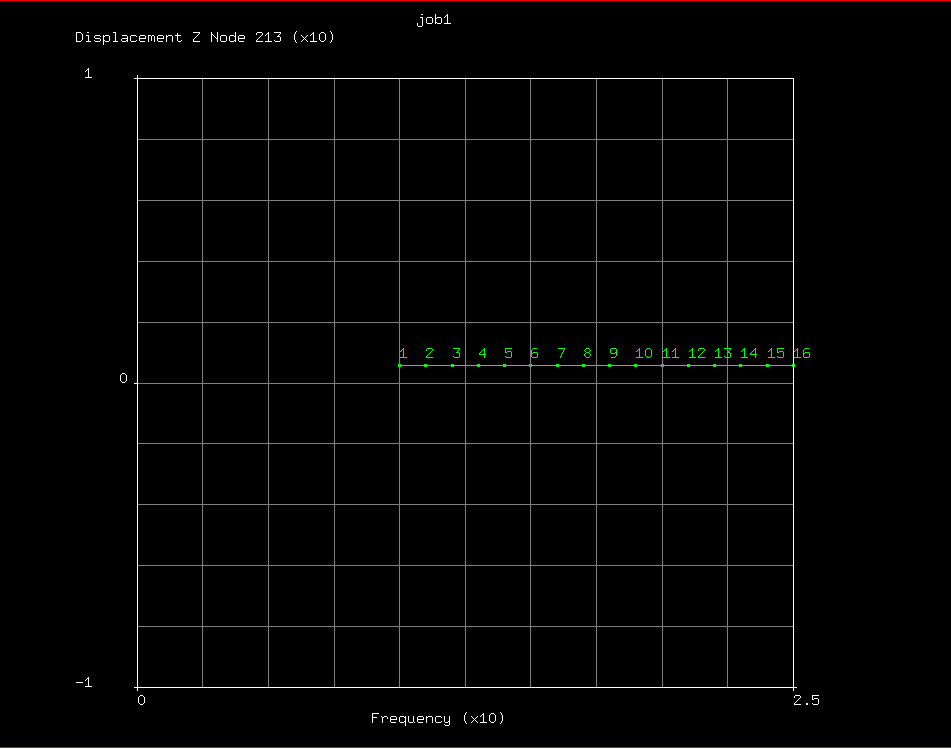
Questo mette in luce un,altra possibile applicazione dell'analisi modale del sistema. Infatti se l'eccitante che andrà a sollecitare la struttura è sufficientemente bassa rispetto la prima frequenza propria allora si potrebbe procedere (in base al grado di accuratezza voluto dall'analisi) allo studio del sistema in caso statico, abbassandone così il costo computazionale e la complessità (matrice massa M=0).
Introduzione dello smorzamento nell'analisi
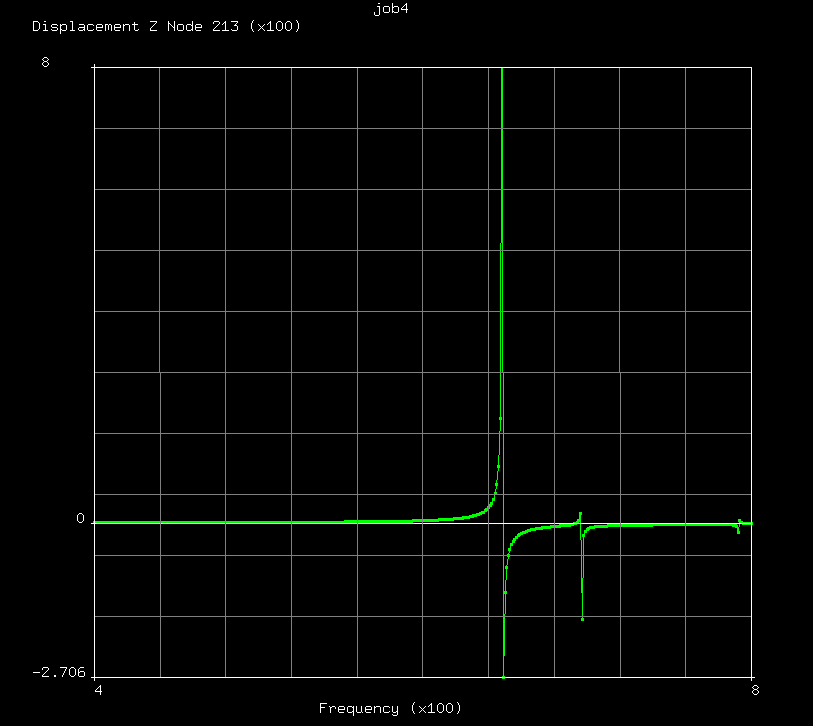 L'analisi svolta fin ora è stata effettuata in assenza di smorzamento. Per questo motivo è possibile effettuare soltanto delle valutazioni qualitative riguardo ai picchi di risonanza osservabili nel grafico. Infatti la loro ampiezza dipende solo dalla prossimità del punto di campionamento alle frequenze proprie del sistema a cui corrispondono dei picchi d'ampiezza infinita. Per questo motivo non è possibile fare nessuna valutazione di tipo ingegneristico.
Inserendo lo smorzamento potrò in seguito andare ad osservare in modo più critico il comportamento della struttura.
L'analisi svolta fin ora è stata effettuata in assenza di smorzamento. Per questo motivo è possibile effettuare soltanto delle valutazioni qualitative riguardo ai picchi di risonanza osservabili nel grafico. Infatti la loro ampiezza dipende solo dalla prossimità del punto di campionamento alle frequenze proprie del sistema a cui corrispondono dei picchi d'ampiezza infinita. Per questo motivo non è possibile fare nessuna valutazione di tipo ingegneristico.
Inserendo lo smorzamento potrò in seguito andare ad osservare in modo più critico il comportamento della struttura.
Rayleigh Damping
Il damping (o smorzamento critico) è definito come: $\zeta = \frac{1}{2}(\frac{\alpha}{2 \pi f}+2 \pi f \beta)$, in funzione quindi dei coefficienti $\alpha$ (contributo della matrice massa alla matrice smorzamento) e $\beta$ ( contributo della matrice rigidezza alla matrice smorzamento). Nel Marc $\alpha$ e $\beta$ sono chiamati rispettivamento MASS MATRIX MULTIPLIER e STIFNESS MATRIX MULTIPLIER.
La scelta del valore di $\zeta$ viene fatta usando opportuni testi di riferimento, in questo caso si sceglie $\zeta=0.01$ supponendo nullo $\alpha$ e di conseguenza il contributo della matrice massa alla matrice smorzamento. Dalla relazione $\zeta = \frac{1}{2}(\frac{\alpha}{2 \pi f}+2 \pi f \beta)$ con $\alpha=0$ ottengo $\beta= 0.01 \cdot g(f)=\frac{0.01}{\pi f}$.
Approfondimenti riguardo i coefficienti del damping possono essere trovati qui.
Comandi Marc
Per inserire uno smorzamento strutturale (es. 1% del critico) occorre seguire i seguenti step:
- accedere al menu
MAIN → MATERIAL PROPERTIES → MATERIAL PROPERTIES; - definire preventivamente una table da menu
TABLES,NEW → 1 INDIPENDENT VARIABLE- settare
TYPEdella Indipendent variable v1 comefrequency
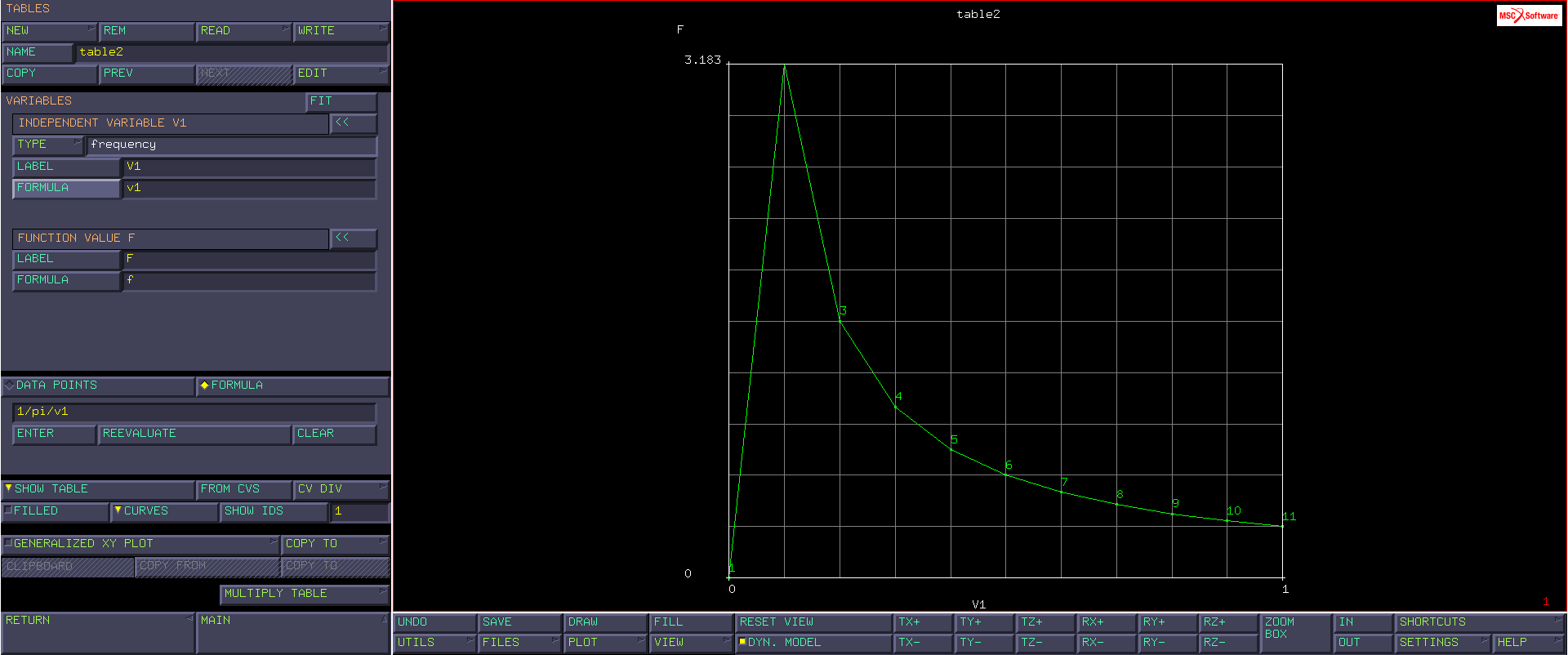
- tornare al menu
MAIN → MATERIAL PROPERTIES → MATERIAL PROPERTIES; - inserire i dati relativi al materiale in esame (“titanio”), quindi entrare nel menu
STRUCTURAL → DAMPINGe attivoDAMPING; - lasciare a valore nullo lo
MASS MATRIX MULTIPLIER - definire uno
STIFFNESS MATRIX MULTIPLIERpari allo smorzamento frazione del critico desiderato, nel caso specifico0.01;
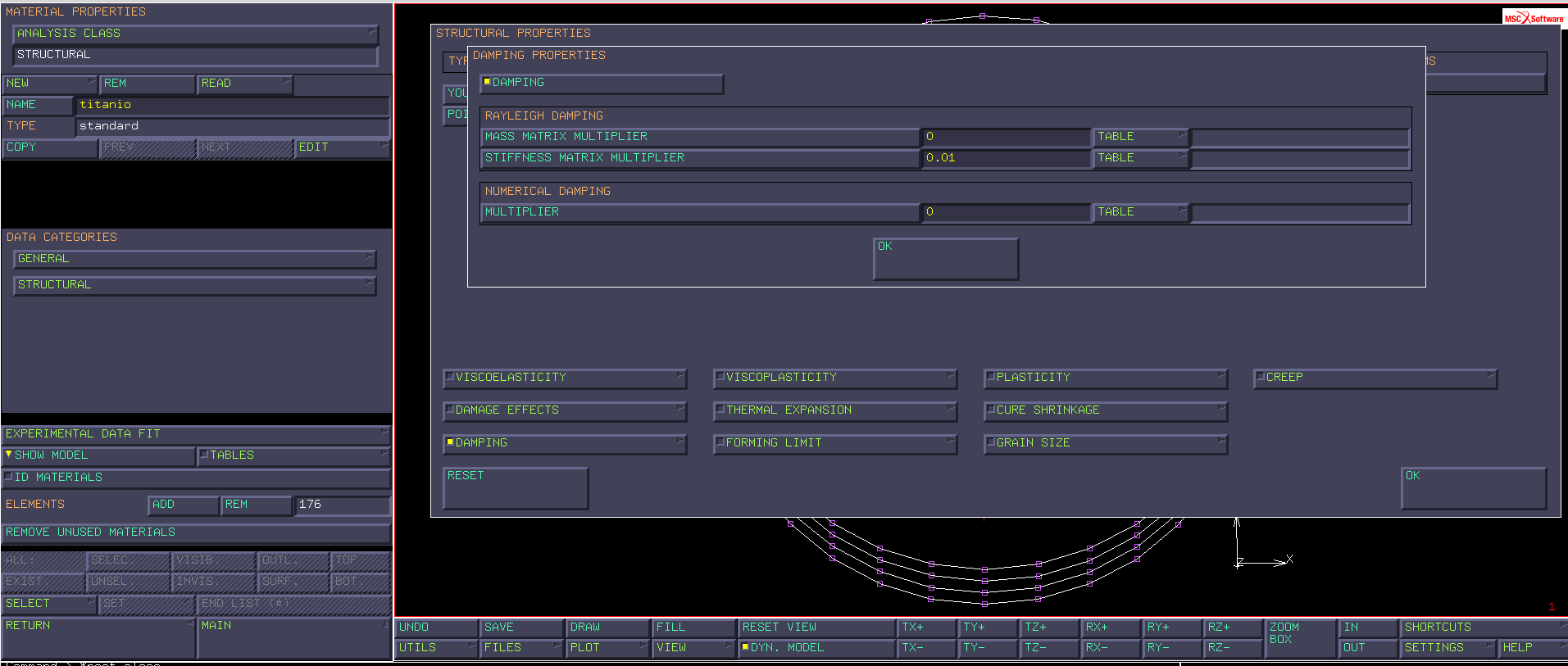
- modularlo tramite una TABLE cliccando sul menu
TABLEche affianca stiffness matrix multiplier - scegliere la table creata precedentemente, quindi cliccare
OKe ancoraOKper tornare al menu “MATERIAL PROPERTIES”; - in questo modo si è definito lo smorzamento fraz. del critico in funzione dei coefficienti $\alpha$ e $\beta$ del Rayleigh damping, supponendo nullo $\alpha$ e quindi il contributo della matrice massa alla matrice smorzamento. In pratica si è ottenuto $\zeta = \frac{1}{2}(\frac{\alpha}{2 \pi f}+2 \pi f \beta)$ con $\alpha=0$ e $\beta= 0.01 \cdot g(f)=\frac{0.01}{\pi f}$, da cui $\zeta=0.01$ come desiderato;
- passare quindi al menu
MAIN → JOBSe creare una copia del job di risposta in frequenza non smorzata selezionandolo e utilizzando il comandoCOPYin alto a sinistra2); - accedere al menu
PROPERTIES, selezionareANALYSIS OPTIONS, attivareCOMPLEX DAMPINGdal blocco dynamic harmonic e quindi confermare conOK; - accedere a
JOB RESULTSe attivareStresseEquivalent von Mises stress; - Si procede quindi a lanciare il calcolo come di consueto da
RUN → SUBMITe aprendo il file dei risultati conOPEN POST FILE (RESULTS MENU); - Si analizza, a titolo di esempio, lo spostamento in direzione $z$ di 5 nodi sulla stessa verticale:
- dal menu POSTPROCESSING
RESULTS, con file dei risultati t16 aperto, procedere entro il menuHISTORY PLOT; - definire i punti di campionamento con
SET LOCATIONS, fornendo quindi al prompt146[invio], seguito da unEND LIST; - definire il range di sotto incrementi di campionamento da
INC RANGE, fornendo quindi al prompt0:1[invio],0:991[invio],1[invio]. Tali valori rappresentano i sotto incrementi di inizio, fine e il passo di campionamento; - procedere a compilare diagrammi sulla base dei dati appena campionati dal menu
ADD CURVES, quindiALL LOCATIONS(si seleziona un solo punto di campionamento). Si compila un grafico che abbia come asse delle ascisse la global variablFrequencye come asse delle ordinateDisplacement Z Magnitudeinfine conFITadatto le scale del grafico alla curva;

- Con
RETURNsi torna al menu HISTORY PLOT dove si può ridurre la frequenza delle etichette indicanti l'incremento portandoSHOW IDSda '1' a '100'; - Benchè il grafico ottenuto non abbia grosse differenze rispetto al precedente, in questo caso i picchi che precedentemente erano solo un indicatore della vicinanza ad una frequenza propria ora assumono un falore che può essere sfruttato per considerazioni ingegneristiche, con oscillazione massima dell'ordine dei 30 mm in corrispondenza della prima pulsazione propria3). È ora visibile che alcuni modi propri, pur non essendo strettamente ortogonali all'eccitante, risultano scarsamente accoppiati e facilmente contenuti da un ridotto smorzamento strutturale.
GRAFICI PER CONSIDERAZIONI DI CARATTERE INGEGNERISTICO
Di seguito vengono riportati alcuni grafici sulla base dei quali è possibile fare alcune considerazioni sulla risposta del sistema.
 Grafico di risposta del sistema smorzato in termini di ampiezza di oscillazione z di un nodo a centro molla in funzione della frequenza del moto eccitante. Occorre verificare le ampiezze di oscillazione tra due sezioni corrispondenti di spire contigue per verificare che non vi sia compenetrazione tra le spire.
Grafico di risposta del sistema smorzato in termini di ampiezza di oscillazione z di un nodo a centro molla in funzione della frequenza del moto eccitante. Occorre verificare le ampiezze di oscillazione tra due sezioni corrispondenti di spire contigue per verificare che non vi sia compenetrazione tra le spire.
 Nel grafico sono riportate le risposte in termini di ampiezza di oscillazione z di un nodo a centro molla in funzione della frequenza del moto eccitante per il caso NON smorzato (curva rossa) e per il caso smorzato (curva verde) con smorzamento 1% del critico. Si nota che nel caso smorzato alcuni picchi di risposta risonante sono ridotti in entità fino ad essere coperti dalle code del modo principale. Si consiglia quindi di inserire un pur piccolo smorzamento (es. 0.0054)) per filtrare i modi risonanti eccitati solo in misura minimale.
Nel grafico sono riportate le risposte in termini di ampiezza di oscillazione z di un nodo a centro molla in funzione della frequenza del moto eccitante per il caso NON smorzato (curva rossa) e per il caso smorzato (curva verde) con smorzamento 1% del critico. Si nota che nel caso smorzato alcuni picchi di risposta risonante sono ridotti in entità fino ad essere coperti dalle code del modo principale. Si consiglia quindi di inserire un pur piccolo smorzamento (es. 0.0054)) per filtrare i modi risonanti eccitati solo in misura minimale.
